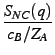Static structure factors S(q) may be compared to experimental scattering data and that is why are useful structural characteristics computed by I.S.A.A.C.S.
Thereafter we describe the theoretical background of S(q)s computed by I.S.A.A.C.S.
Total scattering
Neutron or X-ray scattering static structure factor S(q) is defined as:
where bj and ![]() represent respectively the neutron or X-ray scattering length, and the position of the atom j. N is the total number of atoms in the system studied. To take into account the inherent/volume averaging of scattering experiments it is necessary to sum all possible orientations of the wave vector q compared to the vector
represent respectively the neutron or X-ray scattering length, and the position of the atom j. N is the total number of atoms in the system studied. To take into account the inherent/volume averaging of scattering experiments it is necessary to sum all possible orientations of the wave vector q compared to the vector ![]() -
- ![]() .
.
This average on the orientations of the q vector leads to the famous Debye's equation:
Nevertheless the instantaneous individual atomic contributions introduced by this equation [Eq. 2] are not easy to interpret, It is more interesting to express these contributions using the formalism of radial distribution functions.
In order to achieve this goal it is first necessary to split the self-atomic contribution (j = k), from the contribution between distinct atoms:
with cj =
4π
The function I(q) which describes the interaction between distinct atoms is related to the radial distribution functions through a Fourier transformation:
where the function G(r) is defined using the partial radial distribution functions :
where cα =
G(r) approaches -
Usually the self-contributions are substracted from equation [Eq. 3] and the structure factor is normalized using the relation:
It is therefore possible to write the structure factor [Eq. 4] in a more standard way:
where
In the case of a single atomic species system the normalization allows to obtain values of S(q) and![]() (r) which are independent of the scattering factor/length and therefore independent of the measurement technique. In most cases, however, the total S(q) and g(r) are combinations of the partial functions weighted using the scattering factor and therefore depend on the measurement technique (Neutron, X-rays ...) used or simulated.
(r) which are independent of the scattering factor/length and therefore independent of the measurement technique. In most cases, however, the total S(q) and g(r) are combinations of the partial functions weighted using the scattering factor and therefore depend on the measurement technique (Neutron, X-rays ...) used or simulated.
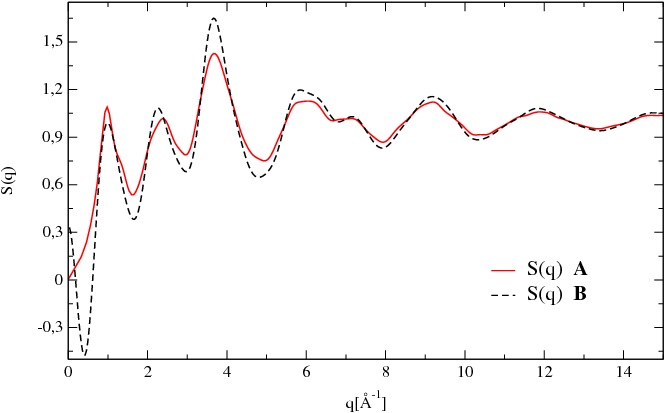
Figure [Fig. 1] presents a comparison bewteen the calculations of the total neutron structure factor done using the Debye relation [Eq. 2] and the pair correlation functions [Eq. 7].
The material studied is a sample of glassy GeS2 at 300 K obtained using ab-initio molecular dynamics.
In several cases the structure factor S(q) and the radial distribution function ![]() (r) [Eq. 8] can be compared to experimental data.
(r) [Eq. 8] can be compared to experimental data.
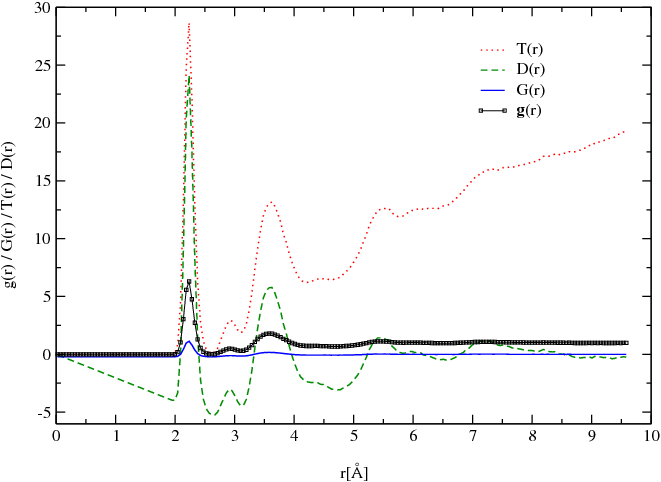
To simplify the comparison I.S.A.A.C.S. computes several radial distribution funcrions used in practice suh as G(r) defined [Eq. 5], the differential correlation function D(r), G(r), and the total correlation function T(r) defined by:
![]() (r) equals zero for r = 0 and approaches 1 for r→∞.
(r) equals zero for r = 0 and approaches 1 for r→∞.
D(r) equals zero for r = 0 and approaches 0 for r→∞.
G(r) equals zero for r = 0 and approaches 0 for r→∞.
T(r) equals zero for r = 0 and approaches ∞ for r→∞.
This set of functions for a model of GeS2 glass (at 300 K) obtained using ab-intio molecular dynamics is presented in figure [Fig. 2].
I.S.A.A.C.S. can compute, for the case of x-ray or neutrons, the following functions:
- S(q) and Q(q) = q[S(q) -1] computed using the Debye equation
- S(q) and Q(q) = q[S(q) -1] computed using the Fourier transform of the
 (r)
(r)  (r) and G(r) computed using the standard real space calculation
(r) and G(r) computed using the standard real space calculation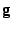 (r) and G(r) computed using the Fourier transform of the structure factor calculated using the Debye equation
(r) and G(r) computed using the Fourier transform of the structure factor calculated using the Debye equation
Partial structure factors
Faber-Ziman definition/formalism
One way used to define the partial structure factors has been proposed by Faber and Ziman [a].
In this approach the structure factor is represented by the correlations between the different chemical species.
To describe the correlation between the α and the β chemical species the partial structure factor SFZαβ(q) is defined by:
where the gαβ(r) are the partial radial distribution functions.
The total structure factor is then obtained by the relation:
Ashcroft-Langreth definition/formalism
In a similar approach, based on the correlation between the chemical species, and developped by Ashcroft et Langreth [b,c,d], the partial structure factors SALαβ(q) are defined by:
where δαβ is the Kronecker delta, cα =
Then the total structure factor can be calculated using:
Bhatia-Thornton definition/formalism
In this approach, used in the case of binary systems ABx [e] only, the total structure factor S(q) can be express as the weighted sum of 3 partial structure factors:where 〈b〉 = cAbA + cBbB, with cA and bA reprensenting respectively the concentration and the scattering length of species A.
SNN(q), SNC(q) and SCC(q) represent combinaisons of the partial structure factors calculated using the Faber-Ziman formalism and weighted using the concentrations of the 2 chemical species:
- SNN(q) is the Number-Number partial structure factor.
Its Fourier transform allows to obtain a global description of the structure of the solid, ie. of the repartition of the experimental scattering centers, or atomic nuclei, positions. The nature of the chemical species spread in the scattering centers is not considered. Furthermore if bA = bB then SNN(q) = S(q).
- SCC(q) is the Concentration-Concentration partial structure factor.
Its Fourier transform allows to obtain an idea of the repartition of the chemical species over the scattering centers described using the SNN(q). Therefore the SCC(q) describes the chemical order in the material. In the case of an ideal binary mixture of 2 chemical species A and B (Particles that can be describe using spheres of the same diameter and occupying the same molar volume, subject to the same thermal constrains, in a mixture where the substitution energy of a partcile by another is equal to zero.), SCC(q) is constant and equal to cAcB. In the case of an ordered chemical mixture (chemical species with distinct diameters, and with heteropolar and homopolar chemical bonds) it is possible to link the variations of the SCC(q) to the product of the concentrations of the 2 chemical species of the mixture:
- SCC(q) = cAcB: radom distribution.
- SCC(q) > cAcB: homopolar atomic correlations (A-A, B-B) prefered.
- SCC(q) < cAcB:heterpolar atomic correlations (A-B) prefered.
- 〈b〉 = 0: SCC(q) = S(q).
- SNC(q) is the Number-Concentration partial structure factor.
Its Fourier transform allows to obtain a correlation between the scattering centers and their occupation by a given chemical species. The more the chemical species related partial structure factors are different ( SAA(q)≠SBB(q)) and the more the oscillations are important in the SNC(q). In the case of an ideal mixture SNC(q) = 0, and all the information about the structure of the system is given by the SNN(q).
cA and ZA représent the concentration and the charge of the chemical species A, the global neutrality of the system must be respected therefore cAZA + cBZB = 0.
Figure [Fig. 3] illustrates, and allows to compare, the partial structure factors of glassy GeS2 at 300 K calculated in the different formalisms Faber-Ziman [a], Ashcroft-Langreth [b,c,d], and Bhatia-Thornton [e].
I.S.A.A.C.S. can compute the following partial structure factors:
- Faber-Ziman
- Ashcroft-Langreth
- Bhatia-Thornton
- a
- T. E. Faber and Ziman J. M.
Phil. Mag., 11(109):153-173 (1965). - b
- N. W. Ashcroft and D. C. Langreth.
Phys. Rev., 156(3):685-692 (1967). - c
- N. W. Ashcroft and D. C. Langreth.
Phys. Rev., 159(3):500-510 (1967). - d
- N. W. Ashcroft and D. C. Langreth.
Phys. Rev., 166(3):934 (1968). - e
- A. B. Bhatia and D. E. Thornton.
Phys. Rev. B, 2(8):3004-3012 (1970).

|
|
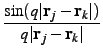
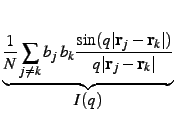
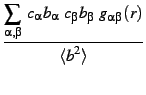
![$displaystyle {frac{{displaystyle{sum_{alpha, beta}} b_alpha b_beta l... ...ha beta}(q) + 1right]}}{{displaystylesum_{alpha} c_alpha b_alpha^2}}}$](images/these-seb/img194.png)
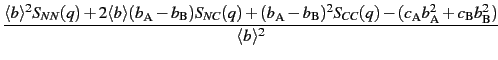 + 1
+ 1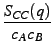 and SNZ(q) =
and SNZ(q) =