Subsections
There are a few, somewhat different definitions of partials S(q) used in practice, and computed by I.S.A.A.C.S.
One way used to define the partial structure factors has been proposed by Faber and Ziman [11].
In this approach the structure factor is represented by the correlations between the different chemical species. To describe the correlation between the α and the β chemical species the partial structure factor
SFZαβ(q) is defined by:
SFZαβ(q) = 1 + 4πρ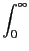 dr r2 dr r2 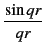 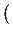 gαβ(r) - 1 gαβ(r) - 1 |
(5.15) |
where the
gαβ(r) are the partial radial distribution functions [Eq. 5.4].
The total structure factor is then obtained by the relation:
S(q) = 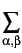 cαbα cβbβ cαbα cβbβ  SFZαβ(q) - 1 SFZαβ(q) - 1![$\displaystyle \left.\vphantom{S^{FZ}_{\alpha \beta}(q) - 1}\right]$](img43.png) |
(5.16) |
In a similar approach, based on the correlation between the chemical species, and developped by Ashcroft et Langreth [12,13,14], the partial structure factors
SALαβ(q) are defined by:
SALαβ(q) = δαβ + 4πρ cαcβ cαcβ 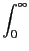 dr r2 dr r2 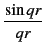 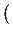 gαβ(r) - 1 gαβ(r) - 1 |
(5.17) |
where
δαβ is the Kronecker delta,
cα = 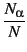 , and the
gαβ(r) are the partial radial distribution functions [Eq. 5.4].
, and the
gαβ(r) are the partial radial distribution functions [Eq. 5.4].
Then the total structure factor can be calculated using:
S(q) = ![$\displaystyle {\frac{{\displaystyle{\sum_{\alpha, \beta}} b_\alpha b_\beta \l...
...ha \beta}(q) + 1\right]}}{{\displaystyle\sum_{\alpha} c_\alpha b_\alpha^2}}}$](img46.png) |
(5.18) |
In this approach, used in the case of binary systems ABx [15] only, the total structure factor S(q) can be express as the weighted sum of 3 partial structure factors:
S(q) =  + 1 + 1 |
(5.19) |
where
〈b〉 = cAbA + cBbB, with
cA and
bA reprensenting respectively the concentration and the scattering length of species
A.
SNN(q), SNC(q) and SCC(q) represent combinaisons of the partial structure factors calculated using the Faber-Ziman formalism and weighted using the concentrations of the 2 chemical species:
SNN(q) =   cAcBSFZAB(q) cAcBSFZAB(q) |
(5.20) |
SNC(q) = cAcB× cA× cA× SFZAA(q) - SFZAB(q) SFZAA(q) - SFZAB(q) - cB× - cB× SFZBB(q) - SFZAB(q) SFZBB(q) - SFZAB(q) ![$\displaystyle \left.\vphantom{ c_\text{A}\times\left(S^{FZ}_{\text{A}\text{A}}...
...t(S^{FZ}_{\text{B}\text{B}}(q) - S^{FZ}_{\text{A} \text{B}}(q)\right) }\right]$](img55.png) |
(5.21) |
SCC(q) = cAcB×![$\displaystyle \left[\vphantom{ 1 + c_{\text{A}} c_{\text{B}} \times \left[ \sum...
...Z}_{\text{A}\text{A}}(q) - S^{FZ}_{\text{A}\text{B}}(q) \right)\right] }\right.$](img56.png) 1 + cAcB× 1 + cAcB×    SFZAA(q) - SFZAB(q) SFZAA(q) - SFZAB(q) ![$\displaystyle \left.\vphantom{ \sum_{\text{A}=1}^{2} \sum_{\text{B}\ne\text{A}}...
...ft( S^{FZ}_{\text{A}\text{A}}(q) - S^{FZ}_{\text{A}\text{B}}(q) \right)}\right]$](img59.png) ![$\displaystyle \left.\vphantom{ 1 + c_{\text{A}} c_{\text{B}} \times \left[ \sum...
...Z}_{\text{A}\text{A}}(q) - S^{FZ}_{\text{A}\text{B}}(q) \right)\right] }\right]$](img60.png) |
(5.22) |
- •
- SNN(q) is the Number-Number partial structure factor.
Its Fourier transform allows to obtain a global description of the structure of the solid, ie. of the repartition of the experimental scattering centers, or atomic nuclei, positions.
The nature of the chemical species spread in the scattering centers is not considered.
Furthermore if
bA = bB then
SNN(q) = S(q).
- •
- SCC(q) is the Concentration-Concentration partial structure factor.
Its Fourier transform allows to obtain an idea of the distribution of the chemical species over the scattering centers described using the SNN(q).
Therefore the SCC(q) describes the chemical order in the material.
In the case of an ideal binary mixture of 2 chemical species A and B5.2, SCC(q) is constant and equal to cAcB.
In the case of an ordered chemical mixture (chemical species with distinct diameters, and with heteropolar and homopolar chemical bonds) it is possible to link the variations of the SCC(q) to the product of the concentrations of the 2 chemical species of the mixture:
-
SCC(q) = cAcB: radom distribution.
-
SCC(q) > cAcB: homopolar atomic correlations (A-A, B-B) prefered.
-
SCC(q) < cAcB: heterpolar atomic correlations (A-B) prefered.
-
〈b〉 = 0:
SCC(q) = S(q).
- •
- SNC(q) is the Number-Concentration partial structure factor.
Its Fourier transform allows to obtain a correlation between the scattering centers and their occupation by a given chemical species.
The more the chemical species related partial structure factors are different (
SAA(q)≠SBB(q)) and the more the oscillations are important in the SNC(q).
In the case of an ideal mixture
SNC(q) = 0, and all the information about the structure of the system is given by the SNN(q).
If we consider the binary mixture as an ionic mixture then it is possible to calculate the Charge-Charge SZZ(q) and the Number-Charge SNZ(q) partial structure factors using the Concentration-Concentration SCC(q) and the Number-Concentration SNC(q):
SZZ(q) =  and SNZ(q) = and SNZ(q) =  |
(5.23) |
cA et ZA represent the concentration and the charge of the chemical species A, the global neutrality of the system must be respected therefore
cAZA + cBZB = 0.
Figure [Fig. 5.6] illustrates, and allows to compare, the partial structure factors of glassy GeS2 at 300 K calculated in the different formalisms Faber-Ziman [11], Ashcroft-Langreth [12,13,14], and Bhatia-Thornton [15].
Figure 5.6:
Partial structure factors of glassy GeS2 at 300 K. A Faber-Ziman [11], B Ashcroft-Langreth [12,13,14] et C Bhatia-Thornton [15].
|
|
I.S.A.A.C.S. can compute the following partial structure factors:
- •
- Faber-Ziman
SFZαβ(q)
- •
- Ashcroft-Langreth
SALαβ(q)
- •
- Bhatia-Thornton SNN(q), SNC(q), SCC(q) and SZZ(q)
Sébastien Le Roux
2011-02-26
